Parity of a permutation
|
Read other articles:

Matoatoa Klasifikasi ilmiah Kerajaan: Animalia Filum: Chordata Kelas: Reptilia Ordo: Squamata Subordo: Lacertilia/Sauria Famili: Gekkonidae Genus: MatoatoaNussbaum, Raxworthy & Pronk, 1998 Matoatoa adalah genus tokek kecil yang tersebar luas di pesisir selatan dan barat daya pulau Madagaskar.[1] Spesies Hanya terdiri dari dua spesies, yaitu:[1] Matoatoa brevipes (MOCQUARD, 1900) Matoatoa spannringi NUSSBAUM, RAXWORTHY & PRONK, 1998 Referensi ^ a b Matoatoa di Reptarium.cz…

لمعانٍ أخرى، طالع بيت الشامي (توضيح). قرية بيت الشامي - قرية - تقسيم إداري البلد اليمن المحافظة محافظة صنعاء المديرية مديرية بني مطر العزلة عزلة بقلان السكان التعداد السكاني 2004 السكان 679 • الذكور 344 • الإناث 335 • عدد الأسر 78 • عدد المساكن 76 …

بوبيني - بابلو بيكاسوBobigny - Pablo Picasso (بالفرنسية) معلومات عامةالتقسيم الإداري بوبيني البلد فرنسا شبكة المواصلات مترو باريس المالك الهيئة المستقلة للنقل في باريس الإدارة الهيئة المستقلة للنقل في باريس الخطوط الخط 5 لمترو باريسالخط 15 لمترو باريس المحطات المجاورة بوبيني - بان�…

Abdullah bin RawahahMakam Abdullah, Zaid bin Haritsah, dan Ja'far bin Abi Thalib di Al-Mazar dekat Mu'tah di YordaniaLahirMadinahMeninggal629Mu'tahSebab meninggalSyahid di Pertempuran Mu'tahMakamAl-Mazar, Mu'tahDikenal atasSahabat NabiOrang tuaRawahah bin Tsa'labah (bapak)Kabsyah binti Waqid (ibu) Abdullah bin Rawahah (Arab: عبد الله بن رواحةcode: ar is deprecated ) adalah salah seorang dari sahabat Nabi Muhammad. Asal dan keluarga Abdullah bin Rawahah bin Tsa'labah bin Imrul …
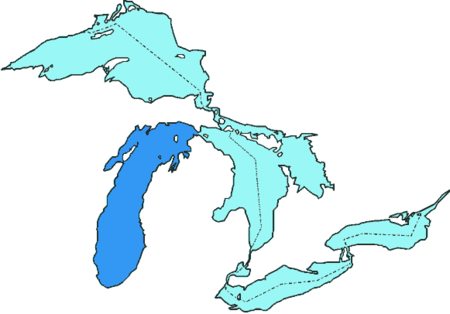
Danau Michigan Danau Michigan ialah salah satu dari 5 Danau-danau Besar di Amerika Utara. Memiliki wilayah permukaan 22.300 mil persegi (57750 km persegi). Panjangnya 307 mil dan luasnya 118 mil. Danau Michigan ialah danau terbesar ke-5 di dunia. Dibatasi oleh negara bagian Amerika Serikat: Indiana, Illinois, Wisconsin, dan Michigan. Kota terbesar di Danau Michigan ialah Chicago. lbsDanau-Danau BesarAmerika Utara(daftar): Danau Superior · Danau Michigan · Danau Huron �…

Untuk anaksungai Tigris, lihat Khabur (Tigris). Sungai Kebar (Khabur) Bahasa Arab: نهر الخابور, Bahasa Aram:ܢܗܪܐ ܕܚܒܘܪ, Bahasa Kurdi: Çemê Xabûr, Bahasa Turki: Habur Nehri, Habor, Chaboras, Bahasa Ibrani Kebar,Chebar sungai Khabur sebelah selatan dari Al-Hasakah Countries Suriah, Turki Kota Ra's al-'Ayn, Al-Hasakah, Busayrah Sumber Ras al-'Ayn - elevation 350 m (1.148 ft) Muara sungai Efrat Panjang 486 km (302 mi) DAS 37.081 km2 (14.317&#…

Dutch cyclist (1918–1973) In this Dutch name, the surname is de Hoog, not Hoog. Henk de HoogHenk de Hoog (1952)Personal informationBorn(1918-08-12)12 August 1918Amsterdam, NetherlandsDied8 May 1973(1973-05-08) (aged 54)Amstelveen, NetherlandsTeam informationRoleRider Henk de Hoog (12 August 1918 – 8 May 1973) was a Dutch racing cyclist. He rode in the 1948 and 1949 Tour de France.[1][2] References ^ 35ème Tour de France 1948 (in French). Memoire du cyclisme. Archive…

Head of Government of Serbia President of the Government of SerbiaПредседник Владе СрбијеPredsednik Vlade SrbijeCoat of arms of SerbiaFlag of SerbiaIncumbentMiloš VučevićActing since 3 April 2024Government of SerbiaStyleHis ExcellencyTypeHead of governmentMember ofGovernmentSeatNemanjina Street 11NominatorThe PresidentAppointerNational AssemblyTerm lengthNo term limitFormation27 August 1805First holderMateja NenadovićUnofficial namesPrime ministerDeputyFirst De…

В Википедии есть статьи о других людях с такой фамилией, см. Соломин. Юрий Соломин Имя при рождении Юрий Мефодьевич Соломин Дата рождения 18 июня 1935(1935-06-18) Место рождения Чита, Восточно-Сибирский край, РСФСР, СССР Дата смерти 11 января 2024(2024-01-11)[1][2] (88 лет) Место смерти М…

LontorNama lokal: Banda BesarBanda Neira dan Lontor dari Banda ApiLontorLokasi di IndonesiaGeografiLokasiLaut BandaKoordinat4°33′S 129°55′E / 4.550°S 129.917°E / -4.550; 129.917KepulauanKepulauan BandaLuas26.37 km2Panjang12 kmLebar3 km Lontor di awal abad kedua puluhLontor tahun 2019 Lontor, juga dikenal sebagai Lonthor atau Lonthoir, atau secara lokal dikenal sebagai Banda Besar, adalah pulau di Kepulauan Banda, Indonesia.[1] Pulau ini dike…

Ecosystem of northeastern China between 133 and 120 million years ago Part of a series onPaleontology Fossils Fossilization Trace fossil Microfossil Fossil preparation Index fossil List of fossils List of fossil sites Lagerstätte fossil beds List of transitional fossils List of human evolution fossils Natural history Biogeography Extinction event Geochronology Geologic time scale Geologic record History of life Origin of life Paleoclimatology Timeline of evolution Transitional fossil Organs and…

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Maret 2016. SMP Negeri 1 AmbonInformasiRentang kelasVII, VIII, IXKurikulumKurikulum Tingkat Satuan PendidikanAlamatLokasiJl. Karang Panjang, Ambon, MalukuMoto SMP Negeri (SMPN) 1 Ambon, merupakan salah satu Sekolah Menengah Pertama Negeri yang ada di Provinsi Maluku, I…

Abat-voix au-dessus de la chaire de l'église Saint-Martin de Dachstein en Alsace. L'abat-voix est une sorte de dôme ou de dais, placé au-dessus de la cuve d'une chaire de vérité, afin de renvoyer la voix du prédicateur vers l'assistance et ainsi en améliorer l'audibilité. Comme les autres parties de la chaire de vérité, l'abat-voix se développa artistiquement, au fil des temps (de l'époque baroque). Ainsi le plafond de l'abat-voix est souvent agrémenté d'une colombe sculptée qui s…

Halaman ini berisi artikel tentang kota di Jawa Timur, Indonesia. Untuk kabupaten bernama sama, lihat Kabupaten Pasuruan. Kota PasuruanKotaTranskripsi bahasa daerah • Hanacarakaꦥꦱꦸꦫꦸꦃꦲꦤ꧀ • Abjad Pegonڤاسوروهن • Péghuڤاسوروواْن • Alfabét Bhâsa MadhurâPhêsoroanMasjid Agung Kota PasuruanRumah Singa Kota Pasuruan LambangJulukan: Pasuruan City of Madinah/ Madinah Van JavaMotto: Sura dira satya pati…

Cet article est une ébauche concernant l’informatique. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Deux utilisateurs accédant à un serveur de fichiers Un serveur de fichiers permet de partager des données à travers un réseau. Le terme désigne souvent l'ordinateur (serveur) hébergeant le service applicatif. Il possède généralement une grande quantité d'espace disque où sont déposés des fichiers. …

John Goodwyn Barmby Bagian dari seriSosialisme Perkembangan Sejarah sosialisme Perdebatan kalkulasi sosialis Ekonomi sosialis Gagasan Penghitungan dalam barang Kepemilikan kolektif Koperasi Kepemilikan bersama Demokrasi ekonomi Perencanaan ekonomi Kesetaraan kesempatan Asosiasi bebas Demokrasi industri Model masukan-keluaran Internasionalisme Kupon kerja Keseimbangan material Ekonomi sejawat ke sejawat(Ekonomi berbagi) Produksi untuk penggunaan Kepemilikan negara Manajemen mandiri Dividen sosial…

German personal care brand that specializes in skin and body care For other uses, see Nivea (disambiguation). This article is in list format but may read better as prose. You can help by converting this article, if appropriate. Editing help is available. (November 2022) NiveaProduct typeSkin and body careOwnerBeiersdorf AGCountryGermanyIntroduced1911 (as Nivea)Related brandsEucerinAquaphorLabelloCoppertoneMarketsWorldwideWebsitenivea.com Nivea (German pronunciation: [niˈveːa] ⓘ,[…

Cet article est une ébauche concernant Los Angeles. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Leimert ParkGéographiePays États-UnisÉtat CalifornieComté comté de Los AngelesCharter city Los AngelesCoordonnées 34° 00′ 28″ N, 118° 19′ 38″ OIdentifiantsGNIS 244720modifier - modifier le code - modifier Wikidata Leimert Park est à la fois le nom d'un quartier et …

Rank comparison chart of Non-commissioned officer and enlisted ranks for navies of Anglophone states. Officers Rank group Senior NCOs Junior NCOs Enlisted Antigua and Barbuda Coast Guard[1]vte Master chief petty officer class 1 Master chief petty officer class 2 Chief petty officer Petty officer Leading seaman Able seaman Royal Australian Navy[2]vte Warrant Officer of the Navy Warrant officer Chief petty officer Petty officer Leading seaman Able seaman Seaman Ro…

Form of creative nonfiction This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Narrative journalism – news · newspapers · books · scholar · JSTOR (April 2021) (Learn how and when to remove this message) This article is written like a personal reflection, personal essay, or argumentative essay that states a Wikiped…














![{\displaystyle {\begin{aligned}\operatorname {sgn}(\sigma \tau )&={\frac {P(x_{\sigma (\tau (1))},\ldots ,x_{\sigma (\tau (n))})}{P(x_{1},\ldots ,x_{n})}}\\[4pt]&={\frac {P(x_{\sigma (1)},\ldots ,x_{\sigma (n)})}{P(x_{1},\ldots ,x_{n})}}\cdot {\frac {P(x_{\sigma (\tau (1))},\ldots ,x_{\sigma (\tau (n))})}{P(x_{\sigma (1)},\ldots ,x_{\sigma (n)})}}\\[4pt]&=\operatorname {sgn}(\sigma )\cdot \operatorname {sgn}(\tau ).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f9e829c1ae788c65317e190d6886600f97dd153)












