Semilattice
|
Read other articles:

Cempaka hutan kasar Bunga Cempaka hutan kasar dan Mandar Dengkur Klasifikasi ilmiah Kerajaan: Plantae Divisi: Magnoliophyta Kelas: Magnoliopsida Ordo: Magnoliales Famili: Magnoliaceae Genus: Elmerrillia Spesies: E. ovalis Cempaka hutan kasar adalah salah satu tanaman identitas Indonesia.[1] Bunga ini merupakan flora endemik khas Sulawesi.[1] Persebaran cempaka hutan kasar meliputi daerah Sulawesi dan Maluku.[1] Nama ilmiah cempaka hutan kasar adalah Elmerrillia ovali…
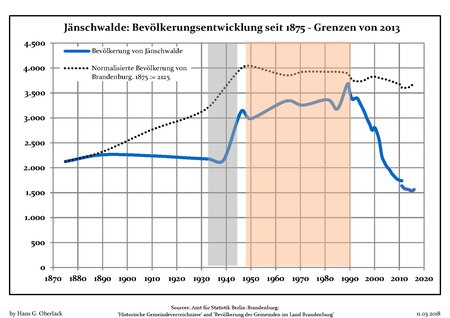
This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Jänschwalde – news · newspapers · books · scholar · JSTOR (December 2009) (Learn how and when to remove this template message) Municipality in Brandenburg, GermanyJänschwalde JanšojceMunicipalityLocation of Jänschwalde within Spree-Neiße district Jänschwalde…

Anika Noni RoseRose di Annual Peabody Awards ke-69, 2010Lahir6 September 1972 (umur 51)Bloomfield, Connecticut, Amerika SerikatPendidikanFlorida A&M University (Sarjana)American Conservatory Theater (Magistrat)PekerjaanPemeran, penyanyiTahun aktif1998–sekarangSitus webtwitter.com/AnikaNoniRose Anika Noni Rose (lahir 6 September 1972) adalah seorang pemeran dan penyanyi Amerika Serikat yang dikenal karena penampilan pemenang Tony Award-nya dalam produksi Broadway Caroline, or Chan…

CIFJenis produkpembersih rumah tanggaPemilikUnileverNegaraPrancisDiluncurkan1969Merek terkaitJif, Vim, Viss, Handy AndyPasar51 negara, GlobalSitus webCif @ Unilever Cif adalah merek produk pembersih rumah tangga oleh Unilever; Yang dikenal sebagai Jif di Australia, Selandia Baru, Timur Tengah dan negara Nordik. Cif merupakan produk pembersih dengan penjualan terbesar abrasif di seluruh dunia. Sejarah Diluncurkan untuk pertama kalinya di Prancis pada tahun 1969, Cif dihadapkan ke pasaran bubuk pe…

H.Tri KurniadiS.H., M.Si.Berkas:Walkot Jaksel Tri Kurniadi.jpg Wali Kota Administrasi Jakarta Selatan ke-14Masa jabatan13 Agustus 2015 – 5 Juli 2018PresidenJoko WidodoGubernurBasuki Tjahaja Purnama Djarot Saiful Hidayat Anies BaswedanWakilArifin PendahuluSyamsuddin NoorPenggantiMarullah MataliWakil Wali Kota Jakarta SelatanMasa jabatan2 Januari 2015 – 13 Agustus 2015PresidenJoko WidodoGubernurBasuki Tjahaja PurnamaWali KotaSyamsuddin Noor PendahuluTri Djoko Sri Margiant…

Koordinat: 43°13′N 27°55′E / 43.217°N 27.917°E / 43.217; 27.917 Varna Варнаcode: bg is deprecated (Bulgaria)Dari kiri atas: Jembatan Asparuh , Pantai Laut Hitam , Euxinograd , Museum Arkeologi Varna , Teater Drama Stoyan Bachvarov , Katedral Bunda Allah , perahu torpedo Drazki , Klub Angkatan Laut, Istana Kebudayaan dan Olahraga , pemandian Romawi kuno, Varna Museum Etnografi BenderaJulukan: Marine (or summer) capital of BulgariaМорска …

Kayu-hitam sulawesi Kayu hitam sulawesi di Palu Klasifikasi ilmiah Kerajaan: Plantae (tanpa takson): Tracheophyta (tanpa takson): Angiospermae (tanpa takson): Eudikotil (tanpa takson): Asterids Ordo: Ericales Famili: Ebenaceae Genus: Diospyros Spesies: D. celebica Nama binomial Diospyros celebicaBakh. f. Kayu-hitam sulawesi adalah sejenis pohon penghasil kayu mahal dari suku eboni-ebonian (Ebenaceae). Nama ilmiahnya adalah Diospyros celebica, yakni diturunkan dari kata celebes (Sulawesi), d…

Stratovolcano in central Mexico Nevado de TolucaNevado de Toluca as seen from Lerma (southeast).Highest pointElevation4,680 m (15,350 ft)[1][2]Prominence2,210 m (7,250 ft)[1][2]Parent peakPopocatépetl[2]Isolation118.39 km (73.56 mi)[1][2]ListingNorth America highest peak 17thNorth America prominent 61stMexico highest major peaks 4thCoordinates19°06′06″N 99°46′03″W / 19.10167°N 9…

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Februari 2023. Fish & Co.IndustriRestoranDidirikan1998KantorpusatSingapuraTokohkunciRicky Choo (pendiri)Lambert Yeo (pendiri)ProdukIkan dan kentang gorengSitus webwww.fish-co.com Fish & Co. adalah sebuah jaringan restoran ikan dan kentang goreng asal Singapura …

United States historic placeOrpheum Theatre and SiteU.S. National Register of Historic Places Show map of IowaShow map of the United StatesLocation405 Main St.Dubuque, IowaCoordinates42°29′52″N 90°39′55″W / 42.49778°N 90.66528°W / 42.49778; -90.66528Built1910ArchitectRapp and RappNRHP reference No.72000474[1]Added to NRHPNovember 14, 1972 Five Flags Center is a multi-purpose facility in downtown Dubuque, Iowa. It is named for the five flags t…

Синелобый амазон Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:ЗавропсидыКласс:Птиц�…

University of California PressPerusahaan indukUniversitas CaliforniaDidirikan1893Negara asalAmerika SerikatKantor pusatOakland, CaliforniaDistribusiIngram Publisher Services (AS)John Wiley & Sons (Britania Raya)Footprint Books (Australia)[1]Jenis terbitanBuku, jurnalSitus resmiwww.ucpress.edu Stan konferensi tahun 2008 University of California Press, juga dikenal sebagai UC Press, adalah sebuah rumah penerbit yang berasosiasi dengan Universitas California yang berfokus dalam bidang p…

Mythological king of Troy Priamus redirects here. For other uses, see Priam (disambiguation). Priam, Last King of TroyKing of TroyScene from the Trojan War: Cassandra clings to the Palladium, the wooden cult image of Athene, while Ajax the Lesser is about to drag her away in front of her father Priam (standing on the left).PredecessorLaomedonPersonal informationParentsLaomedon and Placia or Strymo (or Rhoeo) or Zeuxippe or LeucippeSiblingsTithonus, Lampus, Hicetaon, Clytius, Hesione, Cilla, Asty…

American music magazine SpinKurt Cobain, Courtney Love, and their daughter Frances on Spin, December 1992[1]CategoriesMusicFounded1985; 39 years ago (1985)Final issueSeptember/October 2012; 11 years ago (October 2012) (print)CompanyNext Management PartnersCountryUnited StatesBased inNew York City, New York, U.S.LanguageEnglishWebsitespin.comISSN0886-3032 Spin (stylized in all caps as SPIN) is an American music magazine founded in 1985 by publisher Bob Gucci…

ToyonoboriBirth nameMichiharu SadanoBorn(1931-03-21)March 21, 1931[1]Kanada, Tagawa District, Fukuoka, Japan[2]DiedJuly 1, 1998(1998-07-01) (aged 67)[1]Professional wrestling careerRing name(s)Mr. ZeroToyonoboriBilled height5 ft 9 in (175 cm)Billed weight251 lb (114 kg)Trained byRikidōzanDebutDecember 12, 1954RetiredFebruary 20, 1973 Michiharu Sadano (定野 道春, Sadano Michiharu, March 21, 1931 – July 1, 1998), known in sumo and profes…

6th edition of the Miss Grand United States competition Miss Grand United States 2023Sthephanie Miranda, the winner of the contestDateAugust 17, 2023VenueCrowne Plaza Chicago O'Hare Hotel & Conference Center, Chicago, IllinoisEntrants24Placements15DebutsGreat LakesNew EnglandNortheastTri-StateWest CoastWithdrawalsKansasMaineMinnesotaMississippiReturnsDistrict of ColumbiaGeorgiaHawaiiIllinoisMarylandMichiganMid-AtlanticMissouriNevadaNew JerseyWashingtonWinnerSthephanie Miranda (Great Lakes)Co…

Swedish actress (1925–1994) Mai ZetterlingZetterling from a promotional postcard for Quartet (1948)BornMai Elisabeth Zetterling(1925-05-24)24 May 1925Västerås, SwedenDied17 March 1994(1994-03-17) (aged 68)London, EnglandOccupation(s)Actress, film directorYears active1941–1994Spouses Tutte Lemkow (m. 1944; div. 1953) David Hughes (m. 1958; div. 1979) Children2 Mai Elisabeth Zett…

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: コルク – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL(2017年4月) コルクを打ち抜いて作った瓶の栓 コルク(木栓、蘭&…

Gereja Katolik Bizantin MakedoniaPenggolonganKatolikOrientasiKatolik Timur, Ritus BizantinBentukpemerintahanEpiskopalStrukturEksarkat Apostolik[gci 1]PemimpinUskup Kiro Stojanov[gci 2]WilayahMakedoniaKantor pusatKatedral Maria Diangkat Ke Surga, Strumica, MakedoniaPendiriPaus Yohanes Paulus IIDidirikan2001Terpisah dariEparki KriževciJemaat7 parokiUmat15.037 jiwaRohaniwan11 orang[cnewa 1]Nama lainEksarkat Apostolik Makedonia[gci 1] Bagian dari seri Gereja Katolik …

Questa voce o sezione sull'argomento competizioni calcistiche non cita le fonti necessarie o quelle presenti sono insufficienti. Commento: Fonti assenti Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Questa voce o sezione sull'argomento competizioni calcistiche non è ancora formattata secondo gli standard. Commento: Voce da adeguare al corrispondente modello di voce. …










































