Derived functor
|
Read other articles:

InstagramsoftwareLogoSchermata di esempio GenereSocial network SviluppatoreMeta, Inc. Data prima versione6 ottobre 2010 Ultima versioneAndroid: 221.0.0.16.118[1]iOS, iPadOS: 221.0[2] Sistema operativoiOSAndroidMicrosoft WindowsNon più supportati:Windows 10 MobileWindows Phone LinguaggioPython LicenzaFreeware(licenza non libera) LinguaMultilingua Sito webwww.instagram.com Modifica dati su Wikidata · Manuale Instagram è un servizio di rete sociale statunitens…

This article is about the album. For the juxtaposition of the two attributes, see Ridiculous § Juxtaposition with the sublime. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Sublime to the Ridiculous – news · newspapers · books · scholar · JSTOR (July 2017) (Learn how and when to remove this template mes…

Богослужение Крестного пути или Крестный путь (лат. Via Crucis) — традиционное католическое богослужение, воссоздающее в памяти христиан основные моменты страданий крестного пути Иисуса Христа. Содержание 1 Евангельское повествование 2 Описание богослужения 3 Альтернат…

Anatoly Vasilyevich FilipchenkoLahir(1928-02-26)26 Februari 1928Davydovka, Kegubernuran Voronezh, RSFS Rusia, Uni SovietMeninggal7 Agustus 2022(2022-08-07) (umur 94)KebangsaanSovietPekerjaanPilotPenghargaanPahlawan Uni Soviet (dua kali)Karier luar angkasaKosmonautPangkatMayor Jenderal, Angkatan Udara SovietWaktu di luar angkasa10h 21j 03mSeleksiAir Force Group 2MisiSoyuz 7, Soyuz 16Lambang misi Anatoly Vasilyevich Filipchenko (Rusia: Анато́лий Васи́льевич Фили́пч�…

This article is about the 2003 South Korean drama series. For the South Korean variety show, see Love Letter (variety show). South Korean TV series or program Love LetterLove Letter DVD coverGenreMelodramaRomanceWritten byOh Soo-yeonDirected byOh Kyung-hoonStarringJo Hyun-jaeSoo AeJi Jin-heeCountry of originSouth KoreaNo. of episodes16ProductionProducerJang Geun-sooRunning time60 minutesOriginal releaseNetworkMunhwa Broadcasting CorporationReleaseFebruary 10 (2003-02-10) –April 1, 20…

Ahmad Ramadhan Wakil Kepala Kepolisian Daerah LampungPetahanaMulai menjabat 28 Desember 2023 PendahuluUmar EffendiPenggantiPetahanaKaropenmas Divhumas PolriMasa jabatan17 Desember 2021 – 28 Desember 2023 PendahuluRusdi HartonoPenggantiTrunoyudo Wisnu Andiko Informasi pribadiLahir2 Desember 1969 (umur 54)Bandar Lampung, LampungAlma materAkademi Kepolisian (1991)Karier militerPihak IndonesiaDinas/cabang Kepolisian Daerah LampungMasa dinas1991—sekarangPangkat Brigadi…

Hayato Tani谷隼人LahirHajime IwataniNama lainHayati TaniPekerjaanActorSuami/istriKikko Matsuoka Hayato Tani (谷 隼人 Tani Hayato) (lahir 9 November 1946, dengan nama Hajime Iwatani) adalah seorang aktor film dan televisi asal Jepang. Ia terkenal semenjak memerankan Jenderal Tani dalam game show Benteng Takeshi. Ia juga bermain dalam serial TV Maskman sebagai Komandan Sugata. Saat ini Tani bekerja sebagai penulis artikel makanan dan panduan tatacara makan di Yahoo! Jepang. Di luar itu,…

Historic site in California, United States William B. Ide Adobe State Historic ParkFront of the adobe in 2011Nearest cityRed Bluff, CaliforniaCoordinates40°11′48″N 122°13′31″W / 40.1968°N 122.2252°W / 40.1968; -122.2252Governing bodyState of California California Historical LandmarkReference no.12[1] William B. Ide Adobe State Historic Park is a California State Historic Park located on the west bank of the Sacramento River, a mile north…

Genus of damselflies Echo Echo margarita Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Arthropoda Class: Insecta Order: Odonata Suborder: Zygoptera Family: Calopterygidae Subfamily: Calopteryginae Tribe: Mnaisini Genus: EchoSelys, 1853 Echo is a genus of damselflies belonging to the family Calopterygidae. There are five species.[1] A sixth, Echo maxima, is sometimes included, but it probably belongs to a different genus.[2] This genus is distributed in Asi…

Saturn Award du meilleur film de science-fictionCadreType Récompense du meilleur film par genrePays États-UnisOrganisationSite web (en) www.saturnawards.orgmodifier - modifier le code - modifier Wikidata Le Saturn Award du meilleur film de science-fiction (Saturn Award for Best Science Fiction Film) est une récompense cinématographique décernée chaque année depuis 1973 par l'Académie des films de science-fiction, fantasy et horreur (Academy of Science Fiction Fantasy & Hor…

شروزبوري الإحداثيات 43°31′33″N 72°51′18″W / 43.525833333333°N 72.855°W / 43.525833333333; -72.855 [1] تقسيم إداري البلد الولايات المتحدة[2] التقسيم الأعلى مقاطعة روتلاند خصائص جغرافية المساحة 50.2 ميل مربع ارتفاع 537 متر عدد السكان عدد السكان 1096 (1 أبر�…

Cet article est une ébauche concernant une commune du Puy-de-Dôme. Vous pouvez partager vos connaissances en l’améliorant (comment ?). Le bandeau {{ébauche}} peut être enlevé et l’article évalué comme étant au stade « Bon début » quand il comporte assez de renseignements encyclopédiques concernant la commune. Si vous avez un doute, l’atelier de lecture du projet Communes de France est à votre disposition pour vous aider. Consultez également la page d’aide à…

Water-polo aux Jeux olympiques d'été de 1924 Généralités Sport Water-polo Éditions 6e Lieu(x) Paris Participants ? équipes Épreuves 1 Palmarès Tenant du titre Grande-Bretagne Vainqueur France Deuxième Belgique Troisième États-Unis Navigation Anvers 1920 Amsterdam 1928 modifier L'équipe de France de water-polo, championne olympique en 1924. Résultats du tournoi olympique masculin de Water polo aux Jeux olympiques d'été de 1924 à Paris. Podiums Or Argen…

U.S. Biathlon AssociationAbbreviationUSBAFormation1980TypeNational governing body (NGB)HeadquartersNew Gloucester, Maine, U.S.Region served United StatesAffiliationsInternational Biathlon UnionWebsitewww.teamusa.org/US-Biathlon The United States Biathlon Association (USBA) is the national governing body for Olympic biathlon in the United States and a member of the International Biathlon Union (IBU). The USBA exists to support and encourage the development of biathlon in the United States and to …

Dievs, svētī Latviju (Indonesia: Tuhan Berkatilah Latviacode: id is deprecated ) adalah lagu kebangsaan Latvia dari 1920 -5 Agustus 1940, 21 Agustus 1991-Sekarang adalah sebuah lagu kebangsaan yang dibuat oleh Karlis Baumanis (bahasa Latvia: Baumaņu Kārlis). Dievs, svētī LatvijuB. Indonesia: Tuhan, Berkatilah Latvia!Lagu kebangsaan LatviaPenulis lirikKarlis Baumanis, 1874KomponisKarlis Baumanis, 1873Penggunaan1920 (direstorasikan 1991)Sampel audioLagu kebangsaan Latvia (Inst…

Disambiguazione – Se stai cercando altri significati, vedi Francia (disambigua). Francia (dettagli) (dettagli) (FR) Liberté, Égalité, Fraternité(IT) Libertà, Uguaglianza, Fratellanza Francia - LocalizzazioneLa Francia (verde scuro) nell'Unione europea (verde chiaro) Dati amministrativiNome completoRepubblica francese Nome ufficialeRépublique française Lingue ufficialifrancese Altre linguevedi lista Capitale Parigi (2 229 095[1] ab. / 2018) PoliticaForma…

Questa voce sull'argomento calciatori italiani è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Pierluigi Giunti Nazionalità Italia Calcio Ruolo Portiere Termine carriera 1969 Carriera Squadre di club1 1957-1962 Massese135 (-?)1962-1964 Simmenthal-Monza20 (-?)1964-1966 Rapallo Ruentes57 (-?)1966-1967 L.R. Vicenza6 (-?)1967-1969 Salernitana51 (-36) 1 I due numeri indicano le p…

9th Communication Battalion9th Commmuications Battalion insigniaActive1 June 1966 – presentCountry United States of AmericaBranch United States Marine CorpsTypeCommunicationsPart ofI Marine Expeditionary Force Headquarters GroupNickname(s)9th CommMotto(s)Professionalism, Reliability, FlexibilityEngagementsOperation Desert Storm Operation Restore Hope Operation Iraqi FreedomCommandersCurrentcommanderLtCol Robert A. Doss IIIMilitary unit 9th Communication Battalion (9th Comm) is a comm…
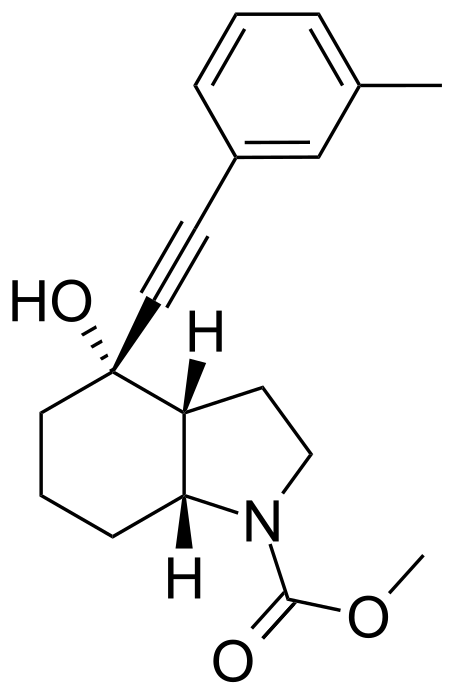
Mavoglurant Names Preferred IUPAC name Methyl (3aR,4S,7aR)-4-hydroxy-4-[(3-methylphenyl)ethynyl]octahydro-1H-indole-1-carboxylate Other names AFQ056 Identifiers CAS Number 543906-09-8 Y 3D model (JSmol) Interactive image ChemSpider 8102466 ECHA InfoCard 100.219.728 IUPHAR/BPS 7586 PubChem CID 9926832 UNII GT0I9SV4F6 CompTox Dashboard (EPA) DTXSID30202777 InChI InChI=1S/C19H23NO3/c1-14-5-3-6-15(13-14)8-11-19(22)10-4-7-17-16(19)9-12-20(17)18(21)23-2/h3,5-6,13,16-17,22H,4,7,9-10,12H2,1-2H3/t16…

Giuliano Alesi Nazionalità Francia Giappone Automobilismo Categoria Super GT Ruolo Pilota Squadra TGR Team au TOM'S Modifica dati su Wikidata · Manuale Giuliano Ryu Alesi (Avignone, 20 settembre 1999) è un pilota automobilistico francese con cittadinanza giapponese di origini italiane Indice 1 Biografia 2 Carriera 2.1 Karting 2.2 Formula 4 francese 2.3 GP3 Series 2.4 Formula 2 2.5 Formula 1 2.6 Corse in Giappone 2.6.1 Super GT 2.6.2 Super Formula 3 Risultati 3.1 Riassun…


























![{\displaystyle (-)^{G}:k[G]{\text{-Mod}}\to k[G]{\text{-Mod}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2123ca8addbb14c40824a2700a9fb9e009519b57)
![{\displaystyle \operatorname {Hom} _{k[G]}(k,-)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/835b77773e277b7aff12dd194e7af55773113cf4)

![{\displaystyle k[G]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a13dacf8d6ff682a6b5d59e84f93e589cba3fa1)
![{\displaystyle H^{i}(G,M)=\operatorname {Ext} _{k[G]}^{i}(k,M)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3c155c5c3b3fb42dc8f288de90c3770ac1c3f73)


















![{\displaystyle (-)_{G}:k[G]{\text{-Mod}}\to k{\text{-Mod}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f04b5aea7ab319ed1f34c1bc1f64111a40702209)
![{\displaystyle k\otimes _{k[G]}-}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c2347a6994bc87a0be4404a8791aeffe30173d76)
![{\displaystyle {\mathfrak {g}}{\text{-Mod}}\to k{\text{-Mod}},M\mapsto M/[{\mathfrak {g}},M]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/10ea68aaf398f81f3affacd1efebbd90d894a499)

![{\displaystyle (A,A){\text{-Bimod}}\to k{\text{-Mod}},M\mapsto M/[A,M]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/83c18b07234f5195adb185affe7d3dfd8e466f8f)





