Moufang loop
|
Read other articles:

Asrama Korps Prajoda pada tahun 1949 Korps Prajoda adalah satu hulptroepen atau kesatuan paramiliter di Bali pada masa Hindia Belanda. Kesatuan ini diawasi dan disupervisi langsung oleh sejumlah perwira KNIL (tentara kolonial Hindia Belanda) yang salah satunya dipimpin oleh perwira Belanda bernama Letnan JBT Konig. Pada tanggal 19 Februari 1942, Jepang mendarat di Bali dan tak ada pasukan KNIL yang tersedia. Hanya saja ada Letnan Kolonel WP. Roodenberg dan Korps Prajoda yang anggotanya berjumlah…

См. также: Живой квест Участники в образе людей викторианской эпохи. Ролевая игра живого действия (от англ. Live action role-playing game, LARP) — разновидность ролевой игры, которая характеризуется непосредственным отыгрышем действий персонажа. Весьма схожа с театральным действие�…

Christian Träsch Informasi pribadiTanggal lahir 1 September 1987 (umur 36)Tempat lahir Ingolstadt, Jerman BaratTinggi 1,80 m (5 ft 11 in)Posisi bermain BekInformasi klubKlub saat ini VfL WolfsburgNomor 15Karier junior1992–2000 TV 1861 Ingolstadt2000–2003 MTV Ingolstadt2003–2006 1860 MunichKarier senior*Tahun Tim Tampil (Gol)2006–2007 1860 Munich II 39 (2)2007–2008 VfB Stuttgart 39 (1)2008–2011 VfB Stuttgart 83 (5)2011– VfL Wolfsburg 17 (0)Tim nasional‡2009–…

AftermathTheatrical release posterSutradaraElliott LesterProduser Darren Aronofsky Peter Dealbert Randall Emmett Scott Franklin George Furla Eric Watson Ditulis olehJavier GullónPemeran Arnold Schwarzenegger Scoot McNairy Maggie Grace Martin Donovan Penata musikMark ToddSinematograferPieter VermeerPenyuntingNicholas Wayman-HarrisPerusahaanproduksi Emmett/Furla/Oasis Films Pacific View Management Protozoa Pictures thefyzz Grindstone Entertainment Group DistributorLionsgate PremiereTanggal …

Dipsadinae Sibon longifrenis (en) TaksonomiKerajaanAnimaliaFilumChordataKelasReptiliaOrdoSquamataFamiliColubridaeSubfamiliDipsadinae Bonaparte, 1838 Tata namaSinonim taksonXenodontinae Cope, 1895 Xenodontidae Cope, 1895 Dipsadidae Bonaparte, 1838lbs Dipsadidae atau yang juga dideskripsikan sebagai Dipsadinae adalah familia ular yang terdiri dari 800 lebih spesies ular. Sejauh ini, diketahui bahwa semua spesies hanya terdapat di Benua Amerika (kecuali daerah dekat Kutub Utara dan Kutub Selatan), …

Artikel ini bukan mengenai Diskografi Hannah Montana. Diskografi Miley CyrusCyrus performing Bottom of the Ocean on the Wonder World Tour.Album studio4Album rekaman langsung1Album kompilasi1Video musik9Extended play1Singel13Album soundtrack5Remix albums2 Artikel ini adalah bagian dari seri tentang Miley Cyrus Diskografi Videografi Lagu Penghargaan Miley Cyrus adalah seorang artis rekaman Amerika. Diskografi nya terdiri dari tiga album studio, tiga album live, dua album kompilasi, dua album remix…

Liaoning Kapal induk Liaoning di Hong Kong pada tahun 2017. Sejarah → Uni Soviet → Ukraina Nama Riga (1988), kemudian Varyag (1990)Asal nama Riga dari kota Riga, Latvia (1988), kemudian Varyag dari Varangia (1990)Dipesan 1983Pembangun Mykolaiv SelatanBiaya US$ 120 Juta (Rp1,87 Triliun) (Bekas Ukraina)Pasang lunas 6 Desember 1985Diluncurkan 4 Desember 1988Selesai Ditelantarkan (68% selesai)Nasib Dijual ke pembeli Tiongkok, 1998; Ditransfer ke angkatan laut Tiongkok, 2002 Sejarah Tiongkok Nama…
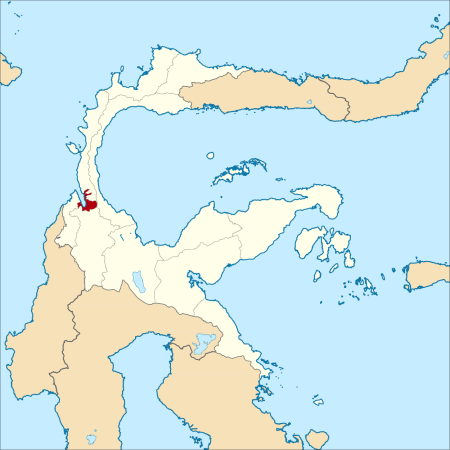
Peta Kota Palu di Sulawesi Tengah Berikut adalah daftar kecamatan dan kelurahan di Kota Palu, Provinsi Sulawesi Tengah, Indonesia. Kota Palu terdiri dari 8 Kecamatan dan 46 Kelurahan dengan luas wilayah 395,06 km² dan jumlah penduduk sebesar 363.867 jiwa dengan sebaran penduduk 921 jiwa/km².[1][2] Sebelumnya, Kota Palu terbagi atas 4 Kecamatan sesuai arah mata angin yaitu Kecamatan Palu Barat, Kecamatan Palu Timur, Kecamatan Palu Utara dan Kecamatan Palu Selatan. Empat kecamata…
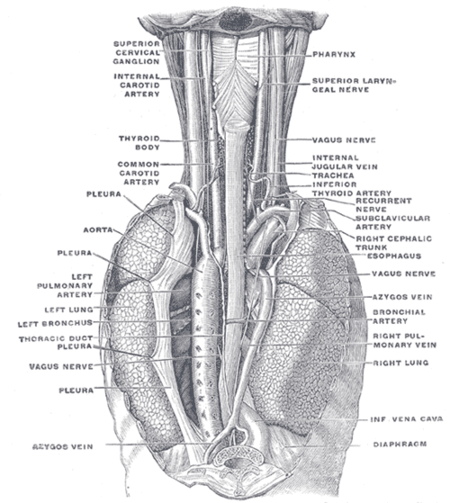
Bagan posisi esofagus pada manusia, dilihat dari belakang Esofagus (dari bahasa Yunani: οiσω, oeso - membawa, dan έφαγον, phagus - memakan) atau kerongkongan adalah tabung (tube) berotot pada vertebrata yang dilalui sewaktu makanan mengalir dari bagian mulut ke dalam lambung. Makanan berjalan melalui esofagus dengan menggunakan proses peristaltik. Esofagus bertemu dengan faring – yang menghubungkan esofagus dengan rongga mulut – pada ruas ke-6 tulang belakang. Menurut histologi, eso…

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Januari 2023. Google Doodle interaktif mengenai Pac-Man sejak tahun 2010 yang akan muncul ketika pengguna mencari google pacman atau play pacman. Perusahaan teknologi Google telah menambahkan easter egg pada berbagai produk dan layanannya, seperti Google Penelusuran, Y…

County building in Truro, Cornwall, England Lys KernowLys Kernow in 2023LocationTruro, CornwallCoordinates50°15′36″N 5°04′09″W / 50.2600°N 5.0692°W / 50.2600; -5.0692Built1966ArchitectFrancis Kenneth Hicklin and Alan GrovesArchitectural style(s)Brutalist style Listed Building – Grade IIDesignated24 April 1998Reference no.1323700 Location of Lys Kernow in Cornwall Lys Kernow, known as New County Hall between 1966 and 2009, is a municipal facility at Trey…
Not to be confused with Football at the Central American Games. Football tournamentFootball at the Central American and Caribbean GamesFounded1930 (men's)2010 (women's)RegionCentral AmericaCaribbeanNumber of teams8 (women's)8 (men's)Current champions Mexico (men's) Mexico (women's)Most successful team(s) Mexico (men's) (7) Mexico (women's) (3) Football at the 2023 Central American and Caribbean Games Association football is one of the sports played at the Central American and…

antv Lampung merupakan stasiun televisi daerah antv yang berada di Bandar Lampung. Siaran antv di Lampung dapat disaksikan di kanal 36 UHF (digital). Sejarah Jika ditilik dari sejarahnya, antv merupakan stasiun televisi swasta pertama yang hadir di Lampung, saat itu sebagai stasiun televisi lokal. Izin siaran stasiun televisi ini didapat 17 September 1991,[1] dan dua tahun kemudian, pada 1 Januari 1993, ANteve memulai siaran percobaannya (di Lampung) selama 5 jam dengan menelan biaya Rp …
TMZURLwww.tmz.comTipeTabloidPerdagangan ?YaRegistration (en)OpsionalLangueInggrisBagian dariWarner Media Group, Telepictures (en), Warner Bros. dan Fox Corporation PemilikFox Corporation Pembuat Harvey Levin Jim Paratore[1] Publisher (en)Harvey LevinService entry (en)8 November 2005; 18 tahun lalu (2005-11-08)[2]Lokasi kantor pusatJefferson Boulevard (en) dan Los Angeles NegaraAmerika Serikat Peringkat Alexa 1497 (Maret 2020[update])[3]KeadaanAktif TMZ (…

This article needs to be updated. Please help update this article to reflect recent events or newly available information. (September 2019) George Washington and Calvin Coolidge on the 1926 Sesquicentennial of American Independence commemorative half dollar Several presidents of the United States have appeared on currency. The president of the United States has appeared on official banknotes, coins for circulation, and commemorative coins in the United States, the Confederate States of America, …

Pour les articles homonymes, voir Berchtold. Leopold BerchtoldFonctionsMinistre des Affaires étrangères d'Autriche-Hongrie17 février 1912 - 13 janvier 1915Alois Lexa von AehrenthalStephan Burián von RajeczAmbassadeur d'Autriche-Hongrie en Russie1906-1911Titre de noblesseComteBiographieNaissance 18 avril 1863Vienne (empire d'Autriche)Décès 21 novembre 1942 (à 79 ans)Peresznye (Sopron, Royaume de Hongrie)Nom dans la langue maternelle Leopold Anton Johann Sigismund Josef Korsinus Ferdin…

Pour les articles homonymes, voir Réforme. Ne doit pas être confondu avec Calendrier grégorien. Grégoire VII, miniature du XIIe siècle. La réforme grégorienne est une politique menée durant le Moyen Âge sous l'impulsion de la papauté. Si les historiens admettent que le pape Léon IX (1049-1054) a commencé le redressement de l'Église, c'est néanmoins le pape Grégoire VII (1073-1085) qui a laissé son nom à la réforme. De plus, les efforts pour sortir l'Église …

Vanillylmandelic acid Names Preferred IUPAC name Hydroxy(4-hydroxy-3-methoxyphenyl)acetic acid Other names 2-Hydroxy-2-(4-hydroxy-3-methoxyphenyl)acetic acidα,4-Dihydroxy-3-methoxybenzeneacetic acidVMAVanillomandelic acidVanillylmandelic acidVanilmandelic acid Identifiers CAS Number 55-10-7 Y 3D model (JSmol) Interactive imageInteractive image Beilstein Reference 2213227 ChEBI CHEBI:20106 Y ChemSpider 1207 Y ECHA InfoCard 100.000.204 EC Number 201-701-6 IUPHAR/BPS 6645 MeSH Vanil…

Sporting event delegationIvory Coast at the2008 Summer OlympicsFlag of Ivory CoastIOC codeCIVNOCComité National Olympique de Côte d'Ivoirein BeijingCompetitors22 in 5 sportsFlag bearer Affoue Amandine AllouMedals Gold 0 Silver 0 Bronze 0 Total 0 Summer Olympics appearances (overview)1964196819721976198019841988199219962000200420082012201620202024 Ivory Coast sent a delegation to compete at the 2008 Summer Olympics in Beijing, China. Athletics Main article: Athletics at the 2008 Summer Oly…

Suku dan bangsa di semenanjung Italia pada abad ke-9 hingga ke-4 SM. Selanjutnya, invasi Galia dan aktivitas pertahanan Republik Romawi membuat perubahan besar di peta. Liguria Venetia Etruria Pikenum Umbria Latin Samnit Messapia Yunani Perkiraan penyebaran bahasa-bahasa di Zaman Besi Semenanjung Italia dan sekitarnya selama abad keenam SM. Umbria adalah salah satu suku Italik yang pernah …





























